ANPEC 2013 - Q7
Anpec 2014 :: MATEMÁTICA :: Questões ANPEC :: Prova 2013
Página 1 de 1
 ANPEC 2013 - Q7
ANPEC 2013 - Q7
Considere a transformação linear 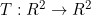 definida por T(x,y)=(x+y,x-ay),
definida por T(x,y)=(x+y,x-ay),  . Denote por A a matriz que representa T na base canônica de R2. Julgue as afirmativas:
. Denote por A a matriz que representa T na base canônica de R2. Julgue as afirmativas:
(0) A matriz associada à transformação T é não singular para a=-1.
F.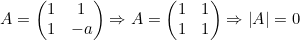
Portanto, A é singular.
(1) Se a=-1, o núcleo de T é um subespaço de dimensão 1.
V. Se a=-1, o posto de A é 1. Como o domínio tem dimensão 2, o núcleo tem dimensão 1.
(2) O sistema Ax=c sempre tem solução para a=1 e c qualquer vetor de R2.
V. Se a=1, o determinante de A é não nulo, portanto o sistema é SPD.
(3) O núcleo e a imagem de T são subespaços cujas dimensões são maiores do que 2.
F. T é um operador linear, de R2 em R2. Pelo Teorema do Núcleo e da Imagem, a soma das dimensões do núcleo e da imagem é a dimensão do domínio que, no caso, é 2.
(4) Para qualquer valor de a o sistema homogêneo Ax=0 tem solução nula.
V. Um sistema homogêneo sempre tem, pelo menos, a solução nula.
(0) A matriz associada à transformação T é não singular para a=-1.
F.
Portanto, A é singular.
(1) Se a=-1, o núcleo de T é um subespaço de dimensão 1.
V. Se a=-1, o posto de A é 1. Como o domínio tem dimensão 2, o núcleo tem dimensão 1.
(2) O sistema Ax=c sempre tem solução para a=1 e c qualquer vetor de R2.
V. Se a=1, o determinante de A é não nulo, portanto o sistema é SPD.
(3) O núcleo e a imagem de T são subespaços cujas dimensões são maiores do que 2.
F. T é um operador linear, de R2 em R2. Pelo Teorema do Núcleo e da Imagem, a soma das dimensões do núcleo e da imagem é a dimensão do domínio que, no caso, é 2.
(4) Para qualquer valor de a o sistema homogêneo Ax=0 tem solução nula.
V. Um sistema homogêneo sempre tem, pelo menos, a solução nula.

temujin- Mensagens : 397
Data de inscrição : 10/03/2013
Anpec 2014 :: MATEMÁTICA :: Questões ANPEC :: Prova 2013
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos|
|
|
