ANPEC 2011 - Q6

por temujin Seg Ago 05, 2013 7:53 pm

Sejam X₁, X₂,...,X_n variáveis aleatórias independentes e normalmente distribuídas, com média 0 e variância σ².

Ⓞ Se σ = 1, a variável Y = ( X₁²+X₂² )/(2X₃² ) possui uma distribuição F com n₁ e n₂ graus de liberdade, para n₁ = 1 e n₂ = 2.

F. Y~F(2,1)

① A variável $W = \frac{X_1}{\sqrt{(X_1^2+X_2^2)/2}}$ possui uma distribuição t com 2 graus de liberdade.

F. Se, e somente, se σ = 1.

② Defina Z = (X₁² + X₂²) /σ². Então E(Z - 2)³ = 0.

F.

$\\ Z \sim \chi^2(2) \Rightarrow E(Z)=2 \\ \\ E(Z - 3)^3 = \frac{E(Z-\mu)^3}{\sigma^3} \neq 0$

Pois o terceiro momento da distribuição é a simetria, e a distribuição qui-quadrado é assimétrica.

③ Suponha que σ = 1 e que H seja uma variável aleatória independente de X₁ e que P(H = 1) = P(H = -1) = 0,5. Então Y = HX₁ ~ N(0,1).

V. Como H e X são independentes, sabemos que Cov(H,X) = 0. Logo,

$E(HX) -E(H).E(X)=0 \Rightarrow E(HX)=E(H).E(X)$

Como X~N(0,1), sabemos que

$E(X)=0 \Rightarrow E(HX)=E(H).0 = 0$

Quanto à variância:

$Var(X) = E(X^2)-[E(X)]^2 \Rightarrow 1=E(X^2)-0 \Rightarrow E(X^2)=1$

Assim:

$\\ Var(HX) = E(H^2X^2)-[E(HX)]^2 \\ \\ H^2 = 1 \Rightarrow Var(HX) = E(X^2)-0^2 \Rightarrow Var(HX)=E(X^2)=1$

Logo, Y~N(0,1).

④ Sabemos que Pr(Z>5165,615)=0,05, onde Z é uma variável aleatória com distribuição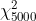 $\chi^2_{5000}$ . Suponha que n = 5001. Defina 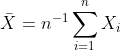$\bar{X}=n^{-1}\sum_{i=1}^nX_i$ e $S^2 = \sum_{i=1}^n(X_i-\bar{X})/(n-1)$ . Se S² = 5,3, pode-se rejeitar a hipótese nula de que σ² = 5 ao nível de significância de 5%.

V.

$Z = \frac{(n-1)S^2}{\sigma^2} = \frac{5000.5,3}{5} = 5300 > 5165,61$

Logo, rejeitamos a hipótese nula.