ANPEC 1991 - Q1
Página 1 de 1
 ANPEC 1991 - Q1
ANPEC 1991 - Q1
Sejam X e Y variáveis aleatórias contínuas com função densidade de probabilidade (f.d.p.) conjunta F(x,y). Então podemos afirmar que:
(0) g(x) =dy) é sempre uma f.d.p. marginal de X.
é sempre uma f.d.p. marginal de X.
V.
(1) Se h(y) =dx) é a f.d.p. marginal de Y, então através de g(x) e h(y) é sempre possível obter a f.d.p. conjunta f(x,y).
é a f.d.p. marginal de Y, então através de g(x) e h(y) é sempre possível obter a f.d.p. conjunta f(x,y).
F. Só se forem independentes. Neste caso, a conjunta é o produto entre as marginais.
(2) Se a distribuição é normal pode-se caracterizar a f.d.p. f(x,y) pelos parâmetros: (I) médias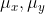 (II) variâncias:
(II) variâncias: 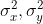 ; (III) correlação de X com Y:
; (III) correlação de X com Y: 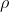 .
.
V. A normal bivariada depende destes 5 parâmetros.
(3) Se X e Y forem independentes então cov(X,Y) = 0.
V.
(4) Se cov(X,Y) = 0 e a distribuição conjunta é normal, então X e Y são independentes.
V. Para a normal bivariada, covariância nula implica independência.
(0) g(x) =
V.
(1) Se h(y) =
F. Só se forem independentes. Neste caso, a conjunta é o produto entre as marginais.
(2) Se a distribuição é normal pode-se caracterizar a f.d.p. f(x,y) pelos parâmetros: (I) médias
V. A normal bivariada depende destes 5 parâmetros.
(3) Se X e Y forem independentes então cov(X,Y) = 0.
V.
(4) Se cov(X,Y) = 0 e a distribuição conjunta é normal, então X e Y são independentes.
V. Para a normal bivariada, covariância nula implica independência.

temujin- Mensagens : 397
Data de inscrição : 10/03/2013
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos|
|
|
