ANPEC 2013 - Q9
2 participantes
Anpec 2014 :: MATEMÁTICA :: Questões ANPEC :: Prova 2013
Página 1 de 1
 ANPEC 2013 - Q9
ANPEC 2013 - Q9
Considere a função 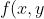=\frac{xy}{x^2+2y^2}) ,
, \neq (0,0) \ e \ f(x,y)=0, \ \ se \ (x,y)=(0,0)) . Julgue as afirmativas:
. Julgue as afirmativas:
(0) A função f é contínua em (0,0).
F. Uma função f é contínua se, e somente se, os limites existem e são iguais ao valor de f no ponto. Para calcular este limite, pode-se usar coordenadas polares:

}\frac{xy}{x^2+2y^2}=\lim_{\rho\rightarrow 0}\frac{\rho cos\theta.\rho sen\theta}{\rho^2 cos^2\theta+2\rho^2 sen^2\theta}=\lim_{\rho\rightarrow 0}\frac{\rho^2 cos\theta sen\theta}{\rho^2 (cos^2\theta +2sen^2\theta)}=\frac{cos\theta sen\theta}{cos^2\theta+2sen^2\theta}\neq 0)
Portanto, f não é contínua em (0,0).
(1) A função f não é diferenciável em (0,0).
V. Ela não é contínua em (0,0), portanto não pode ser diferenciável.
(2) As derivadas parciais na origem existem e são nulas.
V. Na origem, a função f é constante e vale 0. Portanto, as derivadas parciais só podem valer 0.
(3) Existem todas as derivadas parciais de f e, portanto, f é diferenciável em (x,y) para todo (x,y)ER2.
F. A existência das parciais é condição necessária, mas não suficiente. f também precisa ser contínua.
(4) Para todo\neq (0,0), \frac{\partial f}{\partial x}(x,y)=\frac{\partial f}{\partial y}(x,y).)
F. Calculando as derivadas parciais, temos:
-xy.2x}{(x^2+2y^2)^2}=\frac{y(2y^2-x^2)}{(x^2+2y^2)^2})
-xy.4y}{(x^2+2y^2)^2}=\frac{x(x^2-2y^2)}{(x^2+2y^2)^2})
Se tomarmos, por exemplo, (1,1) temos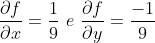
(0) A função f é contínua em (0,0).
F. Uma função f é contínua se, e somente se, os limites existem e são iguais ao valor de f no ponto. Para calcular este limite, pode-se usar coordenadas polares:
Portanto, f não é contínua em (0,0).
(1) A função f não é diferenciável em (0,0).
V. Ela não é contínua em (0,0), portanto não pode ser diferenciável.
(2) As derivadas parciais na origem existem e são nulas.
V. Na origem, a função f é constante e vale 0. Portanto, as derivadas parciais só podem valer 0.
(3) Existem todas as derivadas parciais de f e, portanto, f é diferenciável em (x,y) para todo (x,y)ER2.
F. A existência das parciais é condição necessária, mas não suficiente. f também precisa ser contínua.
(4) Para todo
F. Calculando as derivadas parciais, temos:
Se tomarmos, por exemplo, (1,1) temos

temujin- Mensagens : 397
Data de inscrição : 10/03/2013
 Re: ANPEC 2013 - Q9
Re: ANPEC 2013 - Q9
O item (0) achei melhor responder usando a "Regra dos dois caminhos".
Vagner- Mensagens : 4
Data de inscrição : 08/05/2013
 Re: ANPEC 2013 - Q9
Re: ANPEC 2013 - Q9
Essa eu não conheço...como é isto?

temujin- Mensagens : 397
Data de inscrição : 10/03/2013
 Re: ANPEC 2013 - Q9
Re: ANPEC 2013 - Q9
Tenho um arquivo em PDF explicando, me passa teu email.
Vagner- Mensagens : 4
Data de inscrição : 08/05/2013
Anpec 2014 :: MATEMÁTICA :: Questões ANPEC :: Prova 2013
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos|
|
|
