ANPEC 2010 - Q1

(0) Seja u(x,y) uma utilidade homotética. Suponha que u(x₀,y₀)=u(x₁,y₁), em que (x₀,y₀) e (x₁,y₁) são duas cestas dadas e seja t>0 um escalar positivo. Então, u(tx₀,ty₀)=u(tx₁,ty₁).

V. u(x₀,y₀)=u(x₁,y₁) significa que ambas as cestas estão sobre a mesma CI. E se a função é homotética, o mapa de indiferença é formado por infinitas curvas que são projeções radiais desta CI.


(1) Seja u(x,y) uma utilidade homotética e t>0 um escalar positivo. Denote por TMS_u(x,y) a taxa marginal de substituição da utilidade u na cesta (x,y). Então, TMS_u(x,y)=TMS_u(tx,ty).

V. É uma propriedade das funções homotéticas. Toda CI do mapa de indiferença tem a mesma curvatura.

(2) Seja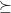 uma relação de preferência monotônica e contínua sobre R²₊ e suponha que u e U são duas funções numéricas que representam a mesma relação de preferência 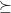.  Suponha que u(x,y) < U(x,y), para qualquer cesta . Se TMS_u(x,y) e TMS_U(x,y) denotam as taxas marginais de substituição de u e U, respectivamente, então TMS_u(x,y)>TMS_U(x,y), para qualquer cesta .

F. Se forem homotéticas, TMS's são iguais!

(3) Considere a função de utilidade u(x,y)=min(2x+y,x+2y} em que x denota a quantidade do bem 1 e y a quantidade do bem 2. Então, os bens 1 e 2 são complementares perfeirtos.

F. Complementares perfeitos têm a forma u(x,y)=min{ax,by}.

(4) Considere a relação binária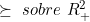 definida por se, e somente se, 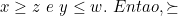é uma relação transitiva e reflexiva, mas não é estritamente monotônica.

V. Esta relação é monotônica se, e somente se, o indivíduo preferir mais de ambos os bens. Mas a relação acima diz que ele prefere menos de y.