ANPEC 2011 - Q2

por temujin Seg Abr 08, 2013 1:55 pm

Considere as retas r₁ e r₂ no plano definidas por 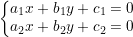$\small \inline \left\{\begin{matrix} a_1x+b_1y+c_1=0\\ a_2x+b_2y+c_2=0 \end{matrix}\right.$ , em que n₁=(a₁,b₁) e n₂=(a₂,b₂) são vetores não nulos ortogonais a r₁ e r₂, respectivamente. Denotamos por d(P,r) a distância de um ponto P a uma reta r do plano. Julgue as afirmativas:

(0) Se as retas r1 e r2 são perpendiculares, então a₁a₂+b₁b₂ = 0

V. Se as retas são perpendiculares, então seus vetores normais serão perpendiculares. Dois vetores são perpendiculares se, e somente se, seu produto escalar é nulo.

(1) Se $\small \inline (1,1) \in r_1$ e r₁ é paralela à reta dada por 2x+3y-6=0, então $\small \inline (3,2) \in r_1$ .

F.

$\small \inline \\ (1,1) \in r_1 \Rightarrow a_1+b_1+c=0 \\ \\ r_1 //r_2 \Rightarrow \vec{nr_1}=\lambda \vec{nr_2} \Rightarrow \vec{nr_1}=\lambda(2,3) \\ \\ 2 \lambda + 3 \lambda+c=0 \Rightarrow c=-5 \lambda \Rightarrow 2\lambda+3\lambda-5\lambda=0\\ \\ \lambda(2,3,-5) \ \therefore \ r_1:2x+3y-5=0 \\ \\ Substituindo \ no \ ponto: \\ \\ 2(3)+3(2)-6=7 \neq 0$

(2) Considere em r₁ os valores c₁=0 e n₁=(1,-1). Se pontos distintos P=(3,y₁) e Q=(3,y₂) são tais que $\small \inline d(P,r_1)=d(Q,r_2)=\sqrt{2}$ , então y₁+y₂=6

V. Pelo vetor normal n₁, sabemos que a equação da reta é dada por: x-y=0. Logo, x=y. Escrevendo a equação na forma vetorial, temos:
$\small \inline (x,y)=\alpha (1,1)$

Os ponto P e Q, fora da reta, podem ser escritos como: $\small \inline \alpha (1,1)+\lambda(1,-1)=(3,y_i)$ , onde $\small \inline |\lambda|.\left \| n_1 \right \|=dist(P,r_1)=dist(Q,r_1)$

Logo, teremos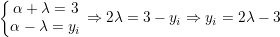 $\small \inline \left\{\begin{matrix} \alpha + \lambda=3\\ \alpha -\lambda=y_i \end{matrix}\right. \Rightarrow 2\lambda=3-y_i \Rightarrow y_i=2\lambda-3$

Sabendo que a norma de n₁ é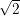 $\small \inline \sqrt{2}$ temos que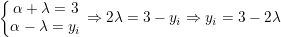 $\small \left\{\begin{matrix} \alpha + \lambda=3\\ \alpha -\lambda=y_i \end{matrix}\right. \Rightarrow 2\lambda=3-y_i \Rightarrow y_i=3-2\lambda$

Existem portanto 2 valores para y_i: y₁= 1 e y₂=5. Então, y₁+y₂=6

(3) As retas y=x, y=1 e y=-x+2 se interceptam formando um triângulo.

F. Elas se inteceptam em apenas um ponto.

$\small \inline y=-x+2 \Rightarrow y=-y+2 \Rightarrow 2y=2 \Rightarrow y=1$

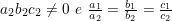(4) Se $\small \inline a_2b_2c_2 \neq 0 \ e \ \frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$ então r₁ e r₂ representam a mesma reta.

V. Neste caso,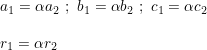 $\small \inline \\ a_1=\alpha a_2 \ ; \ b_1=\alpha b_2 \ ; \ c_1=\alpha c_2 \\ \\ r_1 = \alpha r_2$